参考资料：《CS231n 计算机视觉深度学习》 — CS231n Deep Learning for Computer Vision

什么是神经网络？

简单来说，神经网络（Neural Network） 是一种模仿人脑结构和功能来处理信息、解决问题的计算模型。它是当前人工智能领域，特别是机器学习和深度学习中的核心技术。

神经网络能做什么？

神经网络有强大的模式识别能力，所以在许多领域都有应用，包括但不限于：

• 计算机视觉 (CV)： 人脸识别、自动驾驶车辆识别路标和行人。
• 自然语言处理 (NLP)： 机器翻译（如谷歌翻译）、聊天机器人、情感分析。
• 语音识别： Siri、小爱同学等智能助手的语音识别功能。
• 推荐系统： 淘宝、抖音根据你的喜好推荐商品或视频。

---

神经网络的构成

神经元 (The Neuron)

一个生物神经元通过树突（Dendrites） 接收来自其他神经元的化学信号。如果这些信号累积起来足够强，超过了某个阈值（Threshold），神经元就会被“激活”，并通过其轴突（Axon） 向下游的其他神经元发送一个电信号。

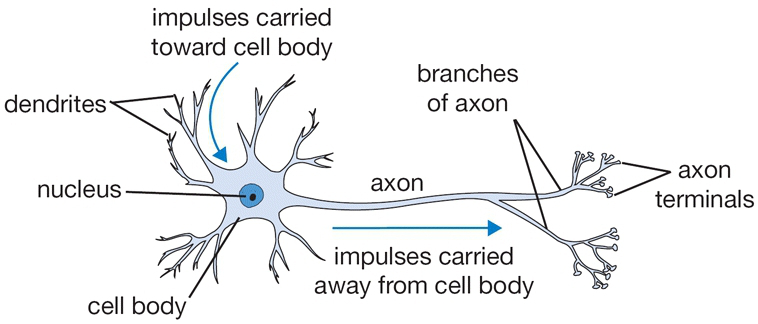
生物神经元

神经网络中的神经元借鉴了生物神经元的核心思想。

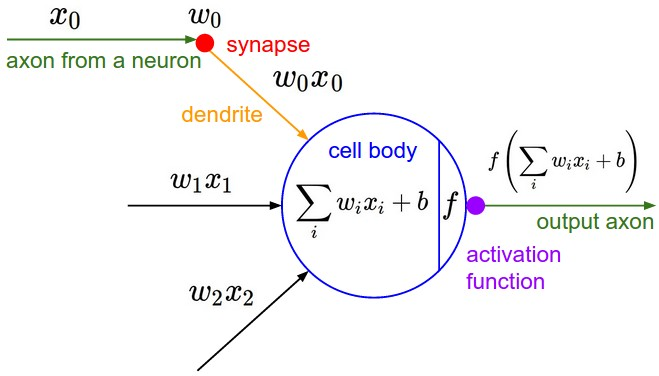
神经网络中的神经元

一个神经网络中的神经元主要由以下三个部分组成：

1. 输入与权重 (Inputs and Weights)
2. 求和与偏置 (Summation and Bias)
3. 激活函数 (Activation Function)

一个神经元是如何处理信息的

第1步：接收带权重的输入
一个神经元会接收一个或多个来自上一层的输入值。这些输入值可以是原始数据（比如图片的像素值），也可以是上一层神经元的输出。每一个输入连接都不是平等的，而是有自己的权重（Weight）。输入 (Inputs, 表示为 $x$): $x_1, x_2, x_3, \dots, x_n$ 权重 (Weights, 表示为 $w$): $w_1, w_2, w_3, \dots, w_n$。权重 $w$ 至关重要，它代表对应输入 $x$ 的重要性。 一个大的正权重意味着这个输入对神经元的激活有很强的促进作用。 一个大的负权重意味着这个输入有很强的抑制作用。 一个接近于0的权重意味着这个输入几乎不起作用。神经网络的学习过程，本质上就是在不断地调整这些权重值。

第2步：加权求和，并加上偏置
神经元会把所有接收到的输入值与它们对应的权重相乘，然后把这些乘积全部加起来。这个过程被称为加权求和。 它会计算一个中间值 $z$，这个 $z$ 值可以看作是神经元接收到的所有信号的“总刺激强度”。 还有一个重要的部分叫做偏置（Bias, 表示为 $b$）。偏置是一个独立的、可学习的数值，它被加到加权和的结果上。 完整的计算公式如下： $$ z = (w_1x_1 + w_2x_2 + \dots + w_nx_n) + b $$ 如果使用向量表示，其中 $\mathbf{w}$ 是权重向量，$\mathbf{x}$ 是输入向量： $$ z = \mathbf{w} \cdot \mathbf{x} + b $$ 可以把偏置理解为神经元固有的激活倾向。它控制着神经元被激活的“难易程度”。 如果偏置 $b$ 是一个很大的正数，那么即使输入的信号不强，神经元也更容易被激活。 如果偏置 $b$ 是一个很大的负数，那么神经元就需要非常强的输入信号才能被激活。

激活函数 (Activation Function)

激活函数一般位于神经元的加权求和之后，负责将计算结果进行一次非线性变换，然后作为该神经元的最终输出传递给下一层。

如果不用激活函数（或使用线性激活函数），那么神经网络的每一层都只是在对输入进行线性变换（$y=wx+b$）。无论你叠加多少层这样的网络，其最终的输出都等同于一个单一的、巨大的线性变换。激活函数的核心作用就是向网络中注入非线性因素。它可以让神经网络打破线性的束缚，获得拟合各种复杂函数的能力，从而能够学习和解决现实世界中的难题。

常见的激活函数

Sigmoid

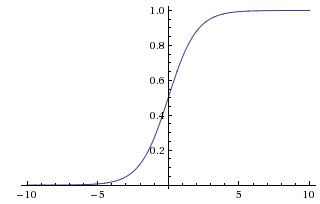
Sigmoid函数

Sigmoid 函数曾被广泛使用，因为它能很好地解释神经元的放电率（从0到1）。但在目前的实践中，它已基本被淘汰。

• 公式:
  $$
  \sigma(x) = \frac{1}{1 + e^{-x}}
  $$
• 特性: 将任意实数压缩到 [0, 1] 的范围内。
• 缺点:
  1. 梯度饱和与消失 (Saturate and kill gradients): 当输入值的绝对值非常大时，Sigmoid 函数的曲线会变得非常平坦，其梯度几乎为零。在反向传播过程中，这个微小的局部梯度会大大削弱梯度的传递，导致网络几乎无法学习。
  2. 输出非零中心 (Outputs are not zero-centered): Sigmoid 的输出值以及梯度恒为正，会导致在反向传播时，权重的梯度要么全部为正，要么全部为负。这会引入“之”字形（zig-zagging）更新动态，降低收敛速度。

Tanh (双曲正切)

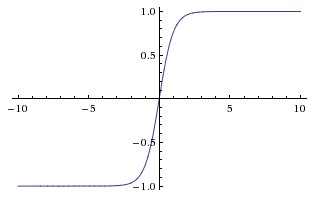
tanh函数

Tanh 函数可以看作是 Sigmoid 函数的一个缩放平移版本，比 Sigmoid 更受青睐。

• 公式:
  $$
  \tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}
  $$
  它与 Sigmoid 的关系为：$\tanh(x) = 2\sigma(2x) – 1$。
• 特性: 将任意实数压缩到 [-1, 1] 的范围内。
• 优点:
  • 输出是零中心的: 相比 Sigmoid，Tanh 的输出以零为中心，这解决了 Sigmoid 的非零中心问题，通常能带来更快的收敛。
• 缺点:
  • 梯度饱和问题: 和 Sigmoid 一样，当输入值的绝对值很大时，Tanh 函数同样会饱和，导致梯度消失的问题。

ReLU (Rectified Linear Unit, 修正线性单元)

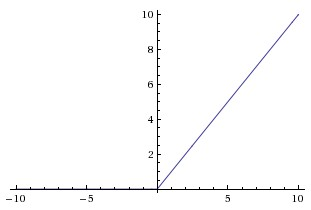
ReLU函数

ReLU 是近年来最受欢迎、最主流的激活函数。它是许多现代神经网络的默认选择。

• 公式:
  $$
  f(x) = \max(0, x)
  $$
• 优点:
  1. 极大加速收敛: 相比 Sigmoid/Tanh，ReLU 在随机梯度下降（SGD）中收敛速度快得多。
  2. 计算高效: 实现起来非常简单。
• 缺点:
  1. 可能“死亡” (Dying ReLU): 在训练过程中，如果一个神经元的权重更新后，使得其对于所有输入数据，加权和总是负数，那么该神经元的输出将永远是0，梯度也永远是0。这个神经元就“死亡”了，无法再参与学习。如果学习率设置不当，网络中可能会有相当一部分神经元“死亡”。

Leaky ReLU

Leaky ReLU 是为了解决“死亡 ReLU”问题而提出的一种变体。

• 公式:
  $$
  f(x) = \max(\alpha x, x)
  $$
  其中 $\alpha$ 是一个很小的正常数，例如 0.01。
• 优点:
  • 修复“死亡”问题: 当输入为负数时，Leaky ReLU 依然有一个微小的、非零的梯度($\alpha$)，这使得“死亡”的神经元有机会“复活”并继续学习。

Maxout

Maxout 是一种更通用的激活函数，它推广了 ReLU 及其变体。

• 公式:
  $$
  \max(\mathbf{w}_1^T \mathbf{x} + b_1, \mathbf{w}_2^T \mathbf{x} + b_2)
  $$
• 优点:
  • 拥有 ReLU 的所有优点: 如线性区、不饱和。
  • 没有“死亡 ReLU”的缺点。
• 缺点:
  • 参数量翻倍: 每个 Maxout 神经元的参数数量是 ReLU 的两倍，导致整个网络的参数总量大幅增加。

网络结构

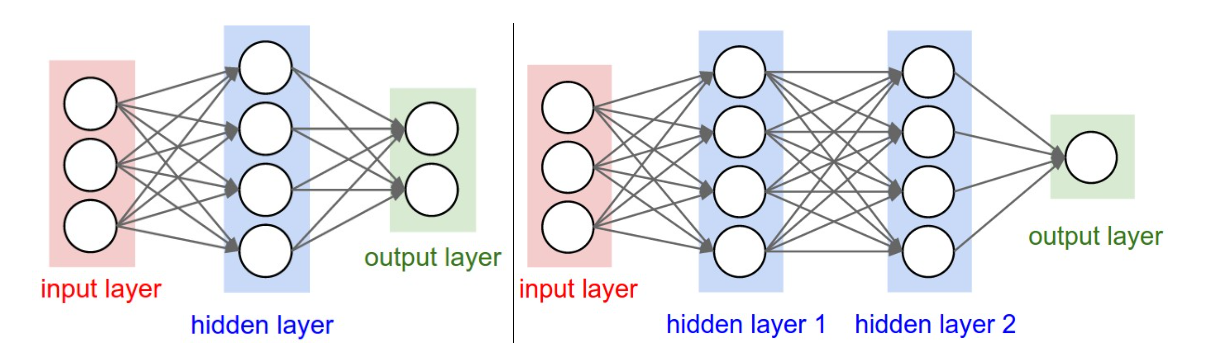
神经网络并非一团杂乱的神经元，而是被清晰地组织在层 (Layers) 中的。信息从第一层开始，依次流向下一层，直到最后一层。在最常见的“常规神经网络”（也叫多层感知机 MLP 或全连接网络）中，层与层之间的关系是全连接 (Fully-connected) 的。这意味着，上一层中的每一个神经元，都与下一层中的所有神经元相连接。但是，在同一层内部，神经元之间没有任何连接。

输入层 (Input Layer)

输入层负责接收最原始的数据。

• 功能：它的任务是接收和传递数据。
• 结构：输入层的神经元数量由数据集的特征数量决定。
  • 例如，如果你的数据是关于房价的，有“面积”、“房间数”和“地理位置”3个特征，那么输入层就有3个神经元。
  • 如果你的数据是一张 28×28 像素的灰度图，那么输入层就需要 28 * 28 = 784 个神经元，每个神经元对应一个像素点。
• 命名规范：在描述一个网络是“N层网络”时，通常不把输入层算在内。所以，一个只有输入层和输出层的网络被称为“单层网络”（逻辑回归就可以看作是单层网络）。

隐藏层 (Hidden Layers)

隐藏层是网络的核心，是进行绝大部分计算和特征提取的地方。

• 功能：隐藏层的神经元接收来自上一层的数据，进行标准的计算（加权求和 + 偏置），然后通过一个非线性的激活函数（如 ReLU）处理，最后将结果输出给下一层。这个过程的本质是特征转换和模式学习。浅层的隐藏层可能学习一些基础特征（如图像的边缘、颜色），而深层的隐藏层则能基于这些基础特征，组合出更复杂的抽象特征（如物体的轮廓、眼睛、鼻子）。
• 结构：隐藏层的数量以及每层神经元的数量是由网络设计者决定的超参数。
  • 隐藏层的数量决定了网络的深度。只有一个隐藏层的网络是“浅层”网络，而有多个隐藏层的网络就是所谓的深度学习 (Deep Learning)网络。
  • 每层神经元的数量决定了网络的宽度。
• 隐藏层既不直接接收外部数据，也不直接向外部输出最终结果。它们的工作过程对用户来说是不可见的，因此被称为“隐藏层”。

输出层 (Output Layer)

输出层是网络的最后一步，负责汇总前面所有层的学习成果，并输出最终的预测结果。

• 功能：产生网络的最终输出。
• 结构：输出层的神经元数量由任务目标决定。
  • 回归任务 (Regression)：例如预测房价，通常只需要 1 个输出神经元，输出一个具体的数值。
  • 二分类任务 (Binary Classification)：例如判断邮件是否为垃圾邮件，也只需要 1 个输出神经元（通常配合 Sigmoid 激活函数，输出一个0到1之间的概率）。
  • 多分类任务 (Multi-class Classification)：例如识别手写数字（0-9），则需要 10 个输出神经元，每个神经元代表一个类别，输出该类别的分数或概率。
• 关于激活函数：与隐藏层不同，输出层通常不使用或使用特定的激活函数。
  • 在回归任务中，输出层通常没有激活函数（或称为线性激活），因为它需要输出任意范围的实数值。
  • 在多分类任务中，输出层通常使用 Softmax 激活函数，它可以将所有神经元的输出转换成一个总和为1的概率分布，便于解释。

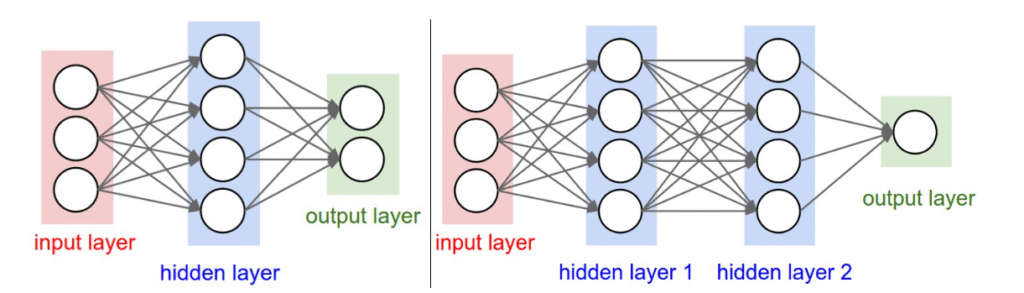
常规神经网络结构示例

如何衡量一个网络的大小？（计算参数）

衡量一个网络规模的常用指标是其可学习参数的数量（即权重和偏置的总和）。
以上图为例。

左侧网络 (2层网络)

• 结构: [输入3] -> [隐藏层4] -> [输出层2]
• 权重:
  • 从输入层到隐藏层：3 * 4 = 12 个
  • 从隐藏层到输出层：4 * 2 = 8 个
  • 总权重：12 + 8 = 20 个
• 偏置: 每个隐藏层和输出层的神经元都有1个偏置。
  • 总偏置：4 + 2 = 6 个
• 总参数: 20 (权重) + 6 (偏置) = 26 个

右侧网络 (3层网络)

• 结构: [输入3] -> [隐藏层4] -> [隐藏层4] -> [输出层1]
• 权重:
  • (输入 -> 隐1): 3 * 4 = 12 个
  • (隐1 -> 隐2): 4 * 4 = 16 个
  • (隐2 -> 输出): 4 * 1 = 4 个
  • 总权重：12 + 16 + 4 = 32 个
• 偏置: 4 + 4 + 1 = 9 个
• 总参数: 32 (权重) + 9 (偏置) = 41 个

常见网络类型

多层感知机 (Multilayer Perceptron, MLP) / 全连接网络 (Fully-Connected Network)

这是最基础的神经网络类型。

• 核心思想：将神经元组织在多个“层”中，上一层的每个神经元都与下一层的所有神经元相连接（即“全连接”）。
• 结构：由一个输入层、一个或多个隐藏层和一个输出层组成。信息从输入层单向地流向输出层。
• 应用场景：处理表格数据、作为更复杂网络的组成部分（例如，CNN的末端分类部分）。它是许多复杂网络的起点和基础。

卷积神经网络 (Convolutional Neural Network, CNN)

CNN在计算机视觉领域有重要作用，它的出现彻底改变了图像处理。

• 核心思想：模仿人类视觉皮层的处理方式，通过“卷积核”（也叫滤波器）来自动学习图像的局部特征。
• 结构：其核心是卷积层 (Convolutional Layer) 和 池化层 (Pooling Layer)。
  • 卷积层：使用一个小的“窗口”（卷积核）在输入图像上滑动，提取像边缘、角点、纹理这样的局部特征，并生成“特征图 (Feature Map)”。
  • 池化层：对特征图谱进行下采样，减少数据量的同时保留最重要的特征，使模型对位置变化不那么敏感（平移不变性）。
• 应用场景：几乎所有与图像相关的任务，如图像分类、目标检测、人脸识别、自动驾驶中的场景识别等。它也成功应用于语音识别和一些文本任务。

循环神经网络 (Recurrent Neural Network, RNN)

RNN是为处理序列数据而生的网络，它的设计考虑了“时间”和“顺序”的概念。

• 核心思想：在网络中引入“记忆”。神经元的输出不仅传递给下一层，还会作为下一次计算的输入，再次传回给自己。这种循环结构使得网络能够记住之前的信息。
• 结构：其核心特征是神经元之间存在循环连接，形成一个内部的“隐藏状态 (Hidden State)”，这个状态就像是网络的短期记忆。
• 应用场景：处理任何与顺序相关的数据。例如：
  • 自然语言处理 (NLP)：机器翻译、文本生成、情感分析（一句话中词语的顺序至关重要）。
  • 时间序列预测：股票价格预测、天气预报。
  • 语音识别。

RNN的重要变体：LSTM 和 GRU

标准的RNN存在长期依赖问题（类似人的短期记忆，很难记住很久以前的事情，会导致梯度消失或爆炸）。为了解决这个问题，两种更强大的变体被提了出来：

• 长短期记忆网络 (Long Short-Term Memory, LSTM)：引入了精巧的“门控机制”（输入门、遗忘门、输出门），像一个可控的传送带，可以选择性地让信息通过、忘记旧信息、添加新信息，从而有效地学习长期依赖关系。
• 门控循环单元 (Gated Recurrent Unit, GRU)：是LSTM的一个简化版本，将三个门合并为两个（更新门和重置门），参数更少，计算效率更高，在许多任务上表现与LSTM相当。

Transformer

Transformer 最初是为机器翻译设计的，但现在已经成为自然语言处理（NLP）领域的绝对主宰，并且其影响力正在向计算机视觉等领域扩展。GPT-3/4 就是基于 Transformer 构建的。

• 核心思想：完全抛弃了RNN的循环结构和CNN的卷积结构，仅依赖于一种叫做“自注意力机制 (Self-Attention)”的机制。
• 结构：核心是自注意力层和前馈网络。自注意力机制能够计算一个句子中所有词语之间的相互重要性，让模型在处理某个词时，能够“关注”到句子中任何其他相关的词，无论它们相距多远。
• 应用场景：所有自然语言处理任务，特别是长文本理解和生成。它是目前最先进的语言模型（如BERT、GPT系列）的基础。

生成对抗网络 (Generative Adversarial Network, GAN)

GAN 是一种非常独特的生成模型，它的目标是创造出以假乱真的新数据。

• 核心思想：博弈论。模型由两个部分组成：一个生成器 (Generator) 和一个判别器 (Discriminator)，它们相互竞争、共同进化。
  • 生成器：努力生成假数据（比如假的人脸图片），试图骗过判别器。
  • 判别器：努力学习如何区分真实数据和生成器生成的假数据。
• 结构：两个独立的神经网络（通常是CNN）相互对抗。生成器的目标是最小化判别器的判断准确率，判别器的目标是最大化自己的判断准确率。
• 应用场景：生成新数据。例如：
  • 生成高清的人脸、动物、艺术品图片。
  • 图像风格迁移。
  • 数据增强。

---

神经网络如何学习？

前向传播与反向传播的流程

前向传播 (Forward Propagation)

这是利用网络进行预测的过程。

• 流程：数据从输入层开始，逐层流向隐藏层，最终到达输出层。在每一层，神经元都会执行标准的计算：接收来自上一层的数据，进行加权求和并加上偏置，然后通过激活函数处理，最后将结果传递给下一层。
• 目标：这个过程的最终目的是计算出网络对输入数据的预测结果，通常用 $\hat{y}$ 来表示。

计算损失

这是量化模型“错误程度” 的过程。

• 流程：将网络在前向传播中得到的预测值 $\hat{y}$ 与真实的标签值 $y$ 进行比较。
• 使用损失函数 (Loss Function) 来计算这两者之间的差距。
  • 回归任务常用均方误差 (MSE)。
  • 分类任务常用交叉熵 (Cross-Entropy)。
• 目标：得到一个具体的数值，即损失值 (Loss) $L$。这个值越大，代表模型的预测错得越离谱；值越小，代表预测越精准。我们的整个训练目标就是让这个损失值尽可能地小。

反向传播 (Backpropagation)

这是整个学习过程中最核心、最关键的一步。它的作用是分配误差责任。

• 流程：将计算出的损失值 $L$ 从输出层开始，沿着网络路径反向传播回输入层。
• 机理：在数学上，它利用了微积分的链式法则 (Chain Rule)。通过这个法则，我们可以高效地计算出总损失 $L$ 对网络中每一个参数（权重 $w$ 和偏置 $b$）的梯度（偏导数），即 $\frac{\partial L}{\partial w}$ 和 $\frac{\partial L}{\partial b}$。
• 目标：计算出所有参数的梯度。这个梯度非常重要，因为它指明了每个参数应该如何调整才能使总损失下降得最快。

更新参数 (Update Parameters)

这是根据反思结果进行修正的过程。

• 流程：既然我们通过反向传播知道了每个参数的梯度，现在就可以对它们进行更新了。
• 我们使用优化器 (Optimizer) 来执行这个更新操作。最基础的优化器就是梯度下降 (Gradient Descent)。
• 机理：参数更新的公式为：
  $$
  w_{\text{new}} = w_{\text{old}} – \eta \frac{\partial L}{\partial w}
  $$
  其中，$\eta$ 是学习率 (Learning Rate)，它控制着每次更新的步长。我们沿着梯度的反方向对参数进行微调。
• 目标：更新网络中所有的权重和偏置，使得网络在下一次接收到相同数据时，计算出的损失会比这一次更小。

重复以上步骤

• 流程：将整个数据集分成若干批次 (batch)，然后不断地重复 步骤1 到 步骤4 的循环。当所有数据都被训练过一遍后，我们称之为一个周期 (Epoch)。通常，一个完整的训练过程需要很多个 Epoch。
• 目标：通过成千上万次的迭代，持续不断地降低损失值，直到它达到一个很低的水平并趋于稳定，这时我们说网络收敛 (converge) 了，训练就完成了。

损失函数 (Loss Function)

什么是损失函数？

在神经网络的训练流程中，我们首先通过前向传播得到一个预测结果 $\hat{y}$。损失函数的核心作用就是量化这个预测结果 $\hat{y}$ 与真实答案 $y$ 之间的差距。

这个计算出的“差值”，称之为损失 (Loss)。

• 损失值很小：说明模型的预测结果和真实结果非常接近，模型表现很好。
• 损失值很大：说明模型的预测结果和真实结果相差甚远，模型表现很差。

因此，整个神经网络训练的最终优化目标，就是通过不断调整网络参数，来最小化损失函数的值。损失函数是反向传播算法的起点，它告诉网络优化的方向。

常见损失函数

选择哪种损失函数，通常取决于要解决的问题类型。下面是两种最主流的损失函数：

均方误差 (MSE – Mean Squared Error)

• 适用场景：主要用于回归问题 (Regression)。回归问题是预测一个连续的数值，例如预测房价、股票价格、气温等。
• 公式:
  $$
  L = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2
  $$
• 公式解读:
  1. $(y_i – \hat{y}_i)$: 计算单个样本的真实值和预测值之间的差值（误差）。
  2. $(…)^2$: 将这个差值平方。这么做有两个好处：
     • 确保结果是正数，因为我们只关心误差的大小，不关心方向（是高了还是低了）。
     • 惩罚大误差。相比于小误差，大误差在平方后会变得不成比例地大，这会迫使模型优先去修正那些错得最离谱的预测。例如，差值为2时，平方后是4；差值为10时，平方后是100。
  3. $\sum_{i=1}^{n}$: 将一个批次中所有样本的平方误差求和。
  4. $\frac{1}{n}$: 取平均值，得到最终的均方误差。这使得损失值的大小与批次大小无关。

交叉熵 (Cross-Entropy)

• 适用场景：主要用于分类问题 (Classification)。分类问题是预测一个物体属于哪个类别，例如图片是猫还是狗，邮件是否为垃圾邮件。
• 核心思想: 衡量两个概率分布之间的差异。在分类任务中，这两个概率分布是：
  1. 真实分布 (y)：即“One-Hot”编码。例如，在一个猫/狗/鸟三分类任务中，一张猫的图片的真实分布是 [1, 0, 0]（100%是猫，0%是狗，0%是鸟）。
  2. 预测分布 ($\hat{y}$)：这是神经网络输出层（通常经过 Softmax 激活函数）给出的预测概率，例如可能是 [0.7, 0.2, 0.1]（70%像猫，20%像狗，10%像鸟）。
• 工作方式: 交叉熵损失函数会衡量这两个概率分布有多“接近”。
  • 如果预测分布和真实分布很接近（如预测 [0.95, 0.03, 0.02]，真实 [1, 0, 0]），交叉熵损失值会非常小。
  • 如果预测分布和真实分布差异很大（如预测 [0.1, 0.8, 0.1]，真实 [1, 0, 0]），交叉熵损失值会非常大。
• 公式 (以多分类为例):
  $$
  L = -\sum_{i=1}^{C} y_i \log(\hat{y}_i)
  $$
  其中，$C$ 是类别的总数，$y_i$ 是真实分布（是该类别则为1，否则为0），$\hat{y}_i$ 是模型预测该类别成立的概率。由于 $y_i$ 中只有一个值为1，其他都为0，所以这个公式实际上只计算了模型对于正确类别的预测概率的对数。模型对正确类别的预测概率 $\hat{y}_i$ 越接近1，$\log(\hat{y}_i)$ 就越接近0，损失 $L$ 就越小。

梯度下降 (Gradient Descent)

在通过损失函数计算出模型的“错误程度”后，我们的目标就是调整网络的参数（权重 $w$ 和偏置 $b$），来让这个“错误”变小。梯度下降就是实现这一目标最经典的方法。

核心思想

梯度下降的核心思想：计算损失函数对于每个参数的梯度，然后沿着梯度的反方向去更新参数，从而一步步找到损失函数的最小值。

超参数

为了有效地更新参数，我们需要知道两个值。

梯度 (Gradient)

• 梯度 $\frac{\partial L}{\partial w}$ 是一个向量，它指向损失函数值增长最快的方向。
• 因此，梯度的反方向 $-\frac{\partial L}{\partial w}$ 就是损失函数值下降最快的方向。
• 这个梯度值是通过反向传播 (Backpropagation) 算法计算出来的。

学习率 (Learning Rate, $\eta$)

学习率是一个非常重要的超参数，它控制着我们每次沿着梯度反方向更新参数时的步长。

• 学习率太大：可能导致振荡 (oscillation)，无法收敛。
• 学习率太小：收敛速度过慢。

选择一个合适的学习率是训练神经网络中最关键的挑战之一。

参数更新

梯度下降的整个过程可以被记成下面这个简单的更新公式。在每一次反向传播之后，网络中的每一个参数都会依据这个公式进行微调：

• 权重更新:
  $$
  w_{\text{new}} = w_{\text{old}} – \eta \frac{\partial L}{\partial w}
  $$
• 偏置更新:
  $$
  b_{\text{new}} = b_{\text{old}} – \eta \frac{\partial L}{\partial b}
  $$

这个公式的含义就是：
新参数 = 旧参数 – 学习率 × 损失对旧参数的梯度

梯度下降的几种变体

在实际应用中，根据计算梯度时使用的数据量不同，梯度下降主要分为三种类型：

• 批量梯度下降 (Batch Gradient Descent)：计算整个训练集的损失后，才计算一次梯度并更新一次参数。优点是方向准确，缺点是当数据集很大时，计算非常缓慢且消耗内存。
• 随机梯度下降 (Stochastic Gradient Descent, SGD)：每处理一个样本，就计算一次梯度并更新一次参数。优点是更新速度快，缺点是更新方向非常不稳定，振荡剧烈。
• 小批量梯度下降 (Mini-Batch Gradient Descent)：这是最实用和常用的方法。它将训练集分成若干个小批次（batch，如每批32或64个样本），每处理完一个小批次，就计算一次梯度并更新一次参数。

反向传播算法 (Backpropagation)

反向传播是一种高效计算梯度的算法，它本质上是链式法则 (chain rule)的应用。梯度指明了函数值增长最快的方向。我们沿着梯度的**相反方向**更新参数，就能最高效地减小损失。
我们可以将复杂的计算过程想象成一个由简单“门”（如加法、乘法）构成的计算图 (Computational Graph)，如下图

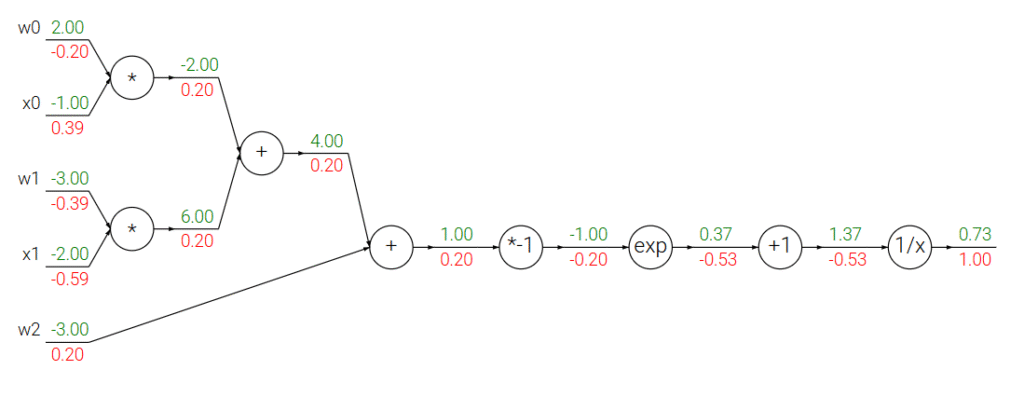
计算图示例

其中绿色数字为前向传播计算出的值，即数据从输入端开始，顺着计算图的方向，一步步计算出所有中间值，直到最终输出（损失值）。
红色数字为反向传播计算出的梯度，即从最终的输出端开始，逆着计算图的方向，利用链式法则递归地计算梯度，我们的目标是计算出最终输出对每一个中间变量和输入的梯度。

示例：$f(x, y, z) = (x + y) \cdot z$

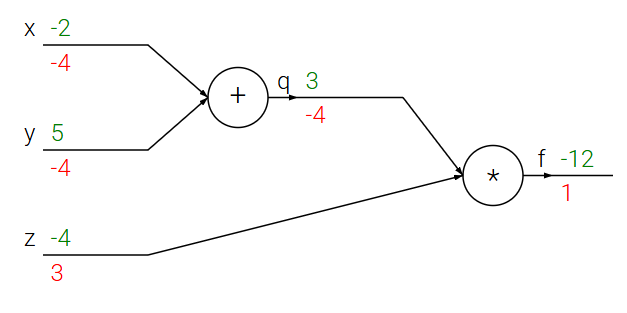
该函数的计算图

1. 分解:
   • $q = x + y$
   • $f = q \cdot z$
2. 前向传播:
   • $x=-2, y=5, z=-4 \rightarrow q=3 \rightarrow f=-12$
3. 反向传播 (链式法则):
   • $\frac{\partial f}{\partial f} = 1$
   • f-q-z 节点: $\frac{\partial f}{\partial q} = z = -4$ | $\frac{\partial f}{\partial z} = q = 3$
   • q-x-y 节点:
   • $\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \cdot \frac{\partial q}{\partial x} = -4 \cdot 1 = -4$
   • $\frac{\partial f}{\partial y} = \frac{\partial f}{\partial q} \cdot \frac{\partial q}{\partial y} = -4 \cdot 1 = -4$

---

神经网络的训练

参数初始化 (Parameter Initialization)

在开始训练神经网络之前，我们必须为网络中所有的参数（权重 $w$ 和偏置 $b$）赋予一个初始值。这个过程就是参数初始化。这个初始值会直接影响到网络的学习速度和最终性能。

为什么参数初始化如此重要？

一个不恰当的初始化可能会导致模型训练失败。其重要性主要体现在以下两点：

打破对称性

• 假设我们将一层中所有的权重都初始化为相同的值（例如，全部初始化为0）。在前向传播时，这一层的所有神经元都会接收到相同的输入，计算出完全相同的输出。在反向传播时，它们会接收到完全相同的梯度，因此它们的权重更新也会完全一样。
• 经过多轮训练，这一层的所有神经元将永远学到完全相同的东西，它们变得毫无区别，就好像这一层实际上只有一个神经元一样。这极大地限制了网络的学习能力。
• 解决方案：我们必须将权重初始化为不同的随机值，来打破这种对称性，使得每个神经元从一开始就有机会去学习网络中不同的特征。

避免梯度消失与梯度爆炸 (Vanishing/Exploding Gradients)

• 在深度神经网络中，信息（前向传播）和梯度（反向传播）需要逐层传递。
  • 梯度消失：如果权重初始值太小，在逐层传递中，信号和梯度会不断衰减，最终在传到浅层网络时变得几乎为0。这会导致浅层网络无法学习。
  • 梯度爆炸：如果权重初始值太大，信号和梯度会逐层放大，最终变得巨大无比，导致数值溢出，训练过程会因不稳定而崩溃。
• 无论哪种情况，都会导致模型无法有效训练。
• 解决方案：我们需要一种更聪明的初始化方法，它能让信号和梯度在网络中传播时，其方差 (Variance) 保持在一个稳定的范围内，既不衰减也不爆炸。

常用的初始化方法

随机初始化 (Random Initialization)

这是最基础的方法，用于解决“打破对称性”的问题。

• 方法：从一个固定的高斯分布（正态分布，例如均值为0，方差为0.01）或均匀分布中随机抽取数值来作为权重的初始值。偏置通常可以初始化为0。
• 优点：简单，能有效打破对称性。
• 缺点：对于深度网络，很难选择一个合适的分布方差。如果方差选得不当，依然很容易陷入梯度消失或爆炸的困境。

Xavier / Glorot 初始化

这是为了解决梯度消失/爆炸问题而提出的一种更科学的方法，由 Xavier Glorot 等人在2010年提出。

• 核心思想：为了让信号在网络中稳定传播，应该让每一层输出的方差和输入的方差尽可能相等。它在推导中同时考虑了前向传播和反向传播的稳定性。
• 方法：它根据一层的输入神经元数量 ($n_{in}$) 和输出神经元数量 ($n_{out}$) 来自动决定初始化的范围。权重的初始化应遵循一个均值为0，方差为 $\text{Var}(W) = \frac{2}{n_{in} + n_{out}}$ 的分布。
  • 实际操作中，通常是从以下分布中随机采样：
    • 均匀分布: $W \sim U\left[-\sqrt{\frac{6}{n_{in} + n_{out}}}, \sqrt{\frac{6}{n_{in} + n_{out}}}\right]$
    • 高斯分布: 均值为0，标准差为 $\sqrt{\frac{2}{n_{in} + n_{out}}}$
• 适用场景：Xavier 初始化在推导时假设激活函数是线性的，因此它对于 Sigmoid 和 Tanh 这类在0点附近近似线性的激活函数效果非常好。但它并不完全适用于 ReLU。

He 初始化 (Kaiming Initialization)

这是由何恺明等人在2015年专门为 ReLU 及其变体设计的初始化方法。

• 核心思想：ReLU 函数的特性（会将所有负数输入置为0）会导致网络中大约一半的神经元输出为0。这意味着在前向传播过程中，信号的方差会减半。为了抵消这个影响，He 初始化在 Xavier 的基础上做出了调整。
• 方法：它只考虑输入神经元数量 ($n_{in}$)。权重的初始化应遵循一个均值为0，方差为 $\text{Var}(W) = \frac{2}{n_{in}}$ 的分布。
  • 实际操作中，通常是从以下分布中随机采样：
    • 高斯分布: 均值为0，标准差为 $\sqrt{\frac{2}{n_{in}}}$
• 适用场景：ReLU、Leaky ReLU、PReLU 等所有基于 ReLU 的激活函数。在现代深度学习中，由于 ReLU 的广泛使用，He 初始化也成为了最常用的初始化方法之一。

优化器 (Optimizers)

梯度下降（Gradient Descent）是优化的基本思想，那么优化器就是将这个思想付诸实践的具体算法。它们是梯度下降的各种改进版本，旨在让模型训练得更快、更稳定。

动量梯度下降 (SGD with Momentum)

• 核心思想: 引入物理学中动量 (Momentum) 的概念来加速学习。
• 工作方式:
  • 它不仅仅依赖于当前批次的梯度来更新参数，而是维护一个“速度”向量（梯度的指数加权平均值）。
  • 每次更新时，参数的改变量是这个“速度”向量，而不是原始的梯度。
  • 如果连续几次的梯度方向大致相同，这个速度会不断累积，使得更新步伐越来越大，从而加速收敛。
  • 如果梯度方向来回摆动，动量可以抵消这些振荡，使更新方向更稳定。
• 优点:
  • 加速收敛：尤其是在梯度方向较为一致的维度上。
  • 帮助冲出局部最小值：惯性使得优化器有能力越过一些浅的局部最优点。

AdaGrad (Adaptive Gradient Algorithm)

• 核心思想: 为不同参数自适应地使用不同的学习率。
• 工作方式:
  • 它会累积每个参数迄今为止所有梯度值的平方和。
  • 在更新参数时，每个参数的学习率会除以这个累积值的平方根。
  • 结果是：梯度历史值越大的参数，其有效学习率就越小；梯度历史值越小的参数，其有效学习率就越大。
• 优点:
  • 能够自适应地为每个参数调整学习率，无需手动调整。
• 缺点:
  • 学习率过早衰减：由于它累积的是所有历史梯度的平方和，这个分母会随着训练的进行不断增大，导致学习率最终会变得无限小，使得模型在后期无法再学到新东西。

RMSprop (Root Mean Square Propagation)

• 核心思想: 对 AdaGrad 的改进，旨在解决其学习率过早衰减的问题。
• 工作方式:
  • 它和 AdaGrad 非常相似，但它在累积梯度平方和时，采用的是指数加权移动平均，而不是简单地将所有历史梯度相加。
  • 这意味着它更关注最近的梯度信息，而会逐渐“忘记”久远的梯度。
  • 这样做的好处是，分母不会再无限地单调递增，从而避免了学习率过早衰减的问题。
• 优点:
  • 解决了 AdaGrad 学习率递减过快的问题。
  • 仍然保留了为不同参数自适应学习率的优点。

Adam (Adaptive Moment Estimation)

• 核心思想: 目前最常用、最主流的优化器之一。它巧妙地结合了 Momentum 和 RMSprop 的优点。
• 工作方式:
  1. 像 Momentum 一样，它计算梯度的指数加权移动平均值（也称为一阶矩估计），这决定了参数更新的“方向”和“速度”。
  2. 像 RMSprop 一样，它计算梯度平方的指数加权移动平均值（也称为二阶矩估计），这为每个参数提供了自适应的学习率。
  3. 它将这两者结合起来，为每个参数计算出独立的、自适应的学习率，同时还带有动量的加速效果。
• 优点:
  • 既有动量的加速效果，又能为每个参数自适应地调整学习率。
  • 在绝大多数问题上都表现得非常好，通常是各种任务的默认首选。
  • 对初始学习率的选择不像其他优化器那么敏感。

过拟合与正则化 (Overfitting & Regularization)

什么是过拟合？

过拟合指的是一个模型在训练数据上表现得过于完美，但在未曾见过的新数据（测试集或验证集） 上表现却很差的现象。

过拟合的模型学到的不是数据中通用的规律（信号），而是特定于训练数据的噪声和细节。它失去了泛化（Generalization） 的能力。

上图中，黑线是好的拟合，而复杂的蓝线就是过拟合。

正则化 (Regularization)：对抗过拟合的策略

正则化是所有用于降低模型复杂度、防止过拟合、提升模型泛化能力的技术的总称。下面是几种最常用和最有效的正则化技术。

L1 / L2 正则化

• 核心思想：一个模型的复杂度通常与其参数（权重）的大小有关。权重值越大，模型可能就越复杂，越容易过拟合。因此，我们可以通过给损失函数增加一个“惩罚项”来限制权重的大小。
  新损失 = 原始损失 + λ * 权重惩罚项
  这里的 $\lambda$ 是一个超参数，用于控制惩罚的力度。
• L2 正则化 (又称“权重衰减”, Weight Decay)
  • 惩罚项：所有权重值的平方和，即 $\lambda \sum w^2$。
  • 效果：它会倾向于让网络中所有的权重值都变得比较小，但不会变为绝对的0。这使得模型的决策边界更平滑，是最常用的正则化方法。
• L1 正则化
  • 惩罚项：所有权重值的绝对值之和，即 $\lambda \sum |w|$。
  • 效果：它会产生稀疏性 (Sparsity)，也就是会使得网络中很多权重值变为精确的0。这相当于让网络自动进行“特征选择”，把一些不重要的特征（对应的权重变为0）剔除掉。

Dropout (随机失活)

• 核心思想：在训练时，不要让任何一个神经元变得“不可或缺”，强迫网络学习到更具鲁棒性和冗余性的特征。
• 工作方式：
  1. 在训练过程中，对于每一个批次的数据，都随机地“丢弃”（即暂时忽略）网络中的一部分神经元（例如，按50%的比例）。
  2. 这意味着这些被丢弃的神经元在这一次的前向传播和反向传播中都不会工作。
  3. 在下一个批次中，又会重新随机选择要丢弃的神经元。
• 效果：由于每次都有不同的神经元被丢弃，任何一个神经元都不能过分依赖于其他特定的神经元。这强迫网络中的每个神经元都要学到一些“真本事”，整个网络会变得更加健壮。
• 注意：Dropout 只在训练时使用。在测试（推理） 时，会使用全部的神经元，以保证模型的最佳性能。

数据增强 (Data Augmentation)

• 核心思想：解决过拟合最根本、最有效的方法就是增加训练数据量。如果无法收集更多真实数据，我们可以通过现有数据创造出更多“新”数据。
• 工作方式：对已有的训练数据进行一系列随机的、不改变其本质标签的变换。
  • 对于图像数据：可以进行随机的旋转、裁剪、水平/垂直翻转、缩放、调整亮度/对比度等。
• 效果：让模型看到同一个物体的各种变体，从而学习到更本质、更不受位置、角度、光照影响的特征，极大地提升了模型的泛化能力。

早停 (Early Stopping)

• 核心思想：在模型开始过拟合的时候，及时停止训练。
• 工作方式：
  1. 将数据分为训练集、验证集 (Validation Set) 和测试集。
  2. 模型在训练集上进行训练，每个周期（Epoch）结束后，在验证集上评估一次性能（如损失或准确率）。
  3. 监控验证集上的性能。通常，训练初期的性能会和训练集一同提升。
  4. 当发现模型在训练集上的性能仍在提升，但在验证集上的性能连续多个周期不再提升，甚至开始下降时，就意味着模型开始过拟合了。
  5. 此时，立即停止训练，并保存验证集上性能最好的那个模型作为最终模型。
• 效果：这是一种非常简单但极其有效的正则化方法，能有效防止模型过度训练。

批处理与周期 (Batch & Epoch)

Epoch (周期)

• 定义：一个 Epoch 指的是所有训练数据完整地通过神经网络一次的过程。
• 由于数据集通常很大，一次性将所有数据都载入内存并进行计算是不现实的。更重要的是，模型仅仅“看”一遍数据，通常不足以学到数据中所有复杂的模式。因此，训练过程需要多个 Epoch，让模型有机会反复学习和优化。
• 一个完整的模型训练通常会持续几十甚至上百个 Epoch，直到模型的性能（如在验证集上的损失）不再有明显提升为止。

Batch Size (批大小)

• 定义：一次梯度更新所使用的样本数量。它决定了我们在将数据“喂”给网络时，一次“喂”多少。
• 这是在计算效率和更新稳定性之间做出的一个权衡。
  • 如果 Batch Size = 整个数据集的大小：这就是“批量梯度下降”。每次更新都基于所有数据，方向最准确，但计算非常缓慢且极其消耗内存，对于大数据集几乎不可行。
  • 如果 Batch Size = 1：这就是“随机梯度下降 (SGD)”。每次更新只基于一个样本，速度很快，但梯度方向非常不稳定（噪声大），会导致训练过程剧烈振荡。
  • Mini-Batch (小批量)：这是最常用的方式。我们选择一个适中的 Batch Size（通常是2的幂，如32, 64, 128, 256），在计算效率和稳定性之间取得了很好的平衡。我们通常说的“Batch”，指的就是 Mini-Batch。

Iteration (迭代)

• 定义：处理完一个 Batch 所需的步骤。每处理完一个 Batch，网络就会进行一次前向传播和一次反向传播，并更新一次参数。这个“更新一次参数”的动作，就是一次迭代。
• 它与 Epoch 和 Batch Size 的关系: 迭代次数是连接 Epoch 和 Batch Size 的桥梁。

它们之间的关系与计算

这三者之间的关系可以用一个简单的公式来表示：

一个周期内的迭代次数 = 训练样本总数 / 批大小

Iterations per Epoch = Total Training Samples / Batch Size

一个具体的例子：

假设我们有一个包含 20,000 张图片的数据集，我们设定的 Batch Size 为 500。

• 一个 Epoch：意味着模型需要处理完这 20,000 张图片。
• 一次 Iteration：模型处理 500 张图片，然后更新一次权重。
• 计算：为了完成一个 Epoch，模型需要进行的迭代次数是：
  20,000 / 500 = 40 次迭代 (Iterations)。

所以，训练过程会是这样：模型读取前500个样本，计算，更新参数（第1次迭代）；接着读取下500个样本，计算，更新参数（第2次迭代）… 这个过程重复40次后，模型就完成了第一个 Epoch。如果我们要训练10个 Epoch，那么总共需要进行的迭代次数就是 40 * 10 = 400 次。